Problem: 1526. 形成目标数组的子数组最少增加次数

递归方法

假设有如下的一个序列:[2,4,3,2,2,1,2,3,2,1]

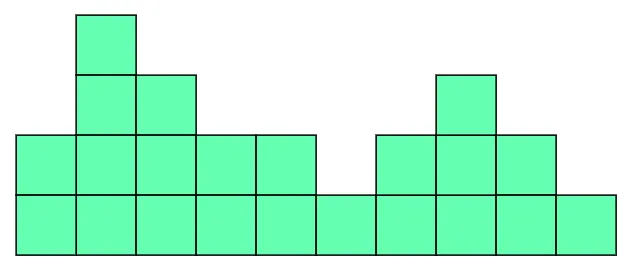
解决思路: 对于每个索引,找到从它往后最后一个数值大于等于它的索引,对于这个图是这样的

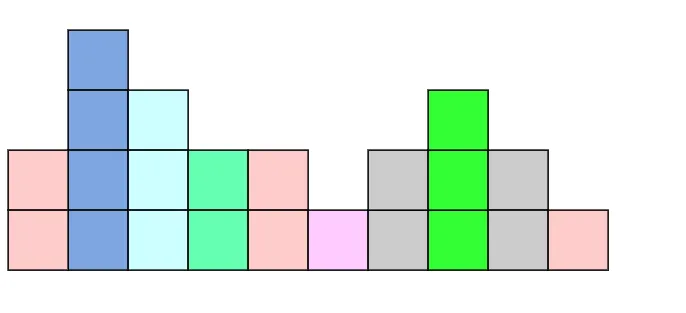这个过程比较好实现,单调栈就可以了

设定一个dfs(left,right,level)->result , 这里, dfs代表的是[left,right]内在level高度下,最少需要多少次.入口为dfs(0,n - 1,0); 在每一个递归中,有如下情况:

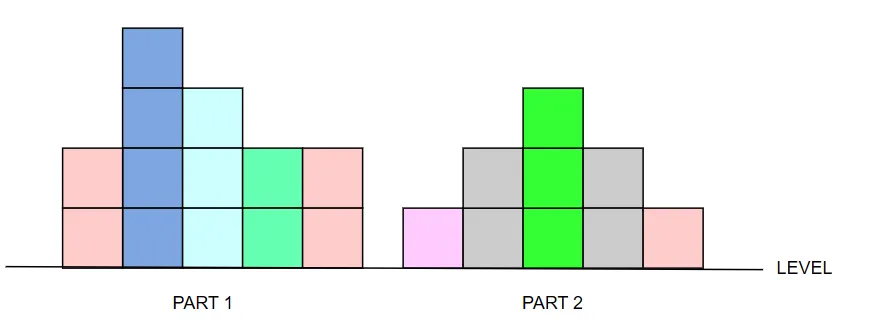
对于PART1,它对于整体的贡献等于 dfs(0,2,2) + 1 这样看不太明显,我们可以画出dfs(0,2,2)的样子:

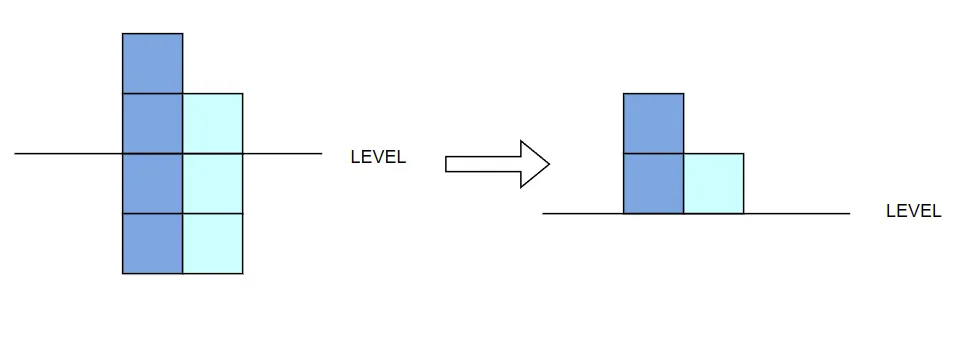
这样依次递归,可以得出dfs(0,2,2) = 2 问题: 这里的1是什么这里的一是指: 相对于这个part右侧第一块的高度和这个part整体高度的差值.对于PART1而言,等于 2 - min(2,1) <=> target[0] - min(target[0],target[5]),所以说如果我们去除1 + dfs(0,2,2) 实际上我们会得到这样的图:

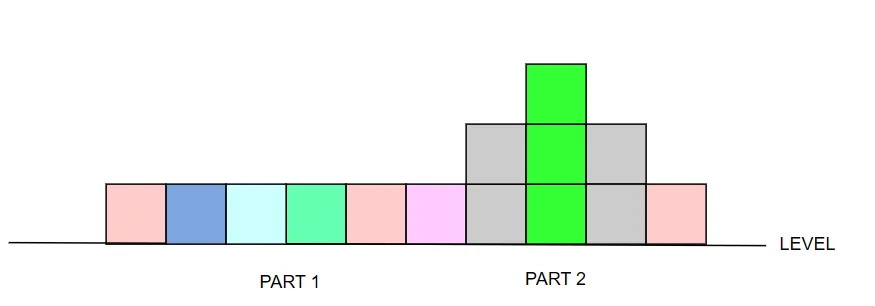
我们在计算PART2时,可以忽略PART1的那一部分,因为此时dfs(0,9,0) = dfs(5,9,0) PART2对于整体的贡献 = target[5] - min(target[5],level) + dfs(6,8,1) = 3 所以说,CONTRIBUTE(PART1) + CONTRIBUTE(PART2) = 6

复杂度

时间复杂度: 𝑂(𝑛) dfs(left,right,level) 每次必然内缩,整个算法每一个idx只会走过一次. 空间复杂度: 𝑂(𝑛)

cpp
class Solution {
public:
    int minNumberOperations(vector<int>& target) {
        int n = target.size();
        vector<int> right_bound(n);
        vector<int> consume(n);
        stack<int> stk;
        for(int i = 0;i < n;i++){
            while(!stk.empty() and target[stk.top()] > target[i]){
                int idx = stk.top();
                right_bound[idx] = i - 1;
                stk.pop();
            }
            stk.emplace(i);
        }
        while(!stk.empty()){
            int idx = stk.top();
            right_bound[idx] = n - 1;
            stk.pop();
        }
        function<int(int,int,int)> dfs = [&](int left,int right,int level){
            if(left > right){
                return 0;
            }
            int ptr = left;
            int res = 0;
            while(ptr <= right){
                int l = ptr;
                int r = min(right,right_bound[ptr]);
                ptr = r + 1;
                int r_next = (r == right) ? level : target[r + 1];
                int standard = target[l] - min(target[l],r_next);
                int num = target[l];
                while(l <= right and target[l] == num){
                    l++;
                }
                while(r >= left and target[r] == num){
                    r--;
                }
                res += standard + dfs(l,r,num);
            }
            return res;
        };
        return dfs(0,n - 1,0); 
    }
};

差分数组

这是一个典型的差分数组的题目,这里不再赘述,只需要统计sum(i if diff[i] > 0 for i in range(0,n))就可以了.

这里的关键之处在于对于任意的[0,r],都有target[r] >= 0,这就保证了,diff前r项中为正的数值一定大于等于为负的数值.

对于这个想法,假设: 对于任意r>=0,remain(0,r)代表只在这一范围内操作,返回值代表没有参与操作的剩余正数之和,这里remain(0,r)一定存在解,让其 >= 0.

要想证明这个,需要证明remain(0,r1) >= sum(abs(diff[i]) for i in range(r2 + 1,r)) (rn代表离r第n远的正数索引)

因为 target[0] + sum(abs(diff[i]) for i in range(1,rn - 1)) >= 0 (target[i] >= 0)

所以 remain(0,rn) >= target[rn],以此类推, remain(0,r1) >= target[r1] remain(0,r1) - sum(abs(diff[i]) for i in range(r2 + 1,r)) >= target[r] >= 0 ,假设成立,[0,r]一定有解,能够将所有diff[i]<0抵消掉.这也是下面统计正数之和能够成立的关键所在.

基于上面的想法,我们对于每个diff[i] >= 0 让其去优先抵消离他最近的diff[i] < 0的地方,通过贪心的方法,找出最优解.

cpp
class Solution {
public:
    int minNumberOperations(vector<int>& target) {
        int n = target.size();
        vector<int> diff(n,0);
        int res = 0;
        diff[0] = target[0];
        if(diff[0] > 0){
            res += diff[0];
        }
        for(int i = 1;i < n;i++){
            diff[i] = target[i] - target[i - 1];
            if(diff[i] > 0){
                res += diff[i];
            }
        }
        return res;
    }
};

作者：barrenham

链接：https://leetcode.cn/problems/minimum-number-of-increments-on-subarrays-to-form-a-target-array/solutions/3819236/di-gui-chai-fen-shu-zu-by-tender-jonesn4-ox18/ 来源：力扣（LeetCode）

著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

目录

递归方法

复杂度

差分数组